Reactancia inductiva y capacitiva
Por Luis A. del Molino EA3OG (ea3og@ure.es)
En el ABC DE LAS ANTENAS, el capítulo 7º está dedicado a los problemas que nos da una ROE (Relación de Ondas Estacionarias) elevada en la antena y en la línea de transmisión, problemas que se derivan casi siempre de antenas demasiado cortas o demasiado largas, es decir, que no tienen exactamente la media longitud de onda requerida para la resonancia y, como consecuencia, no presentan la impedancia correcta deseada (igual que la impedancia característica del cable) en su punto de alimentación, en el que por consiguiente aparecen además reactancias capacitivas o inductivas adicionales.
Cuando hablo de las antenas NO resonantes y de la aparición de una reactancia en ellas, siempre tengo el temor de que les suene a chino a todos los radioaficionados que no han estudiado nada de electricidad y electrónica. Por eso he pensado que valía la pena intentar explicar lo mejor posible en nuevo artículo el significado físico de la reactancia, para que se comprenda bien su presencia en las antenas. Así que este artículo va dedicado a todos aquellos que no lo han entendido bien todavía, porque no han asistido nunca a un curso de electricidad o electrónica, o no se lo han explicado nunca bien.
Aunque en el título aparece en primer lugar la reactancia inductiva, como es mucho más fácil de visualizar la reactancia capacitiva que la inductiva, voy a empezar por el condensador, y a examinar su carga y descarga en corriente continua y en alterna, porque luego esto me servirá para explicar más fácilmente la reactancia causada por la autoinducción de una bobina, diciendo que ocurre exactamente lo mismo, pero de modo opuesto de lo que sucede en un condensador y esto ayudará a visualizarla mejor.
El condensador
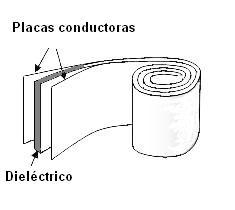
Recordemos que un condensador está formado por dos láminas conductoras (a las que llamamos armaduras), separadas y aisladas entre sí por un dieléctrico (un material aislante, o sea no conductor) de forma que quedan muy próximas y paralelamente enfrentadas (figura 1).
Los condensadores almacenan cargas de signo positivo y negativo en sus placas a medida que aplicamos una tensión a las dos láminas. La conectada al lado negativo se llena de electrones (-) y la conectada al lado positivo se vacía de electrones (Figura 2) y la llamamos carga positiva (+), aunque supongo que ya sabéis que solo se mueven realmente los electrones. Oído al detalle de que exactamente la misma cantidad de electrones que salen de una placa, entra en la placa opuesta, y a eso le llamamos carga positiva, aunque realmente es la falta de electrones..
 |
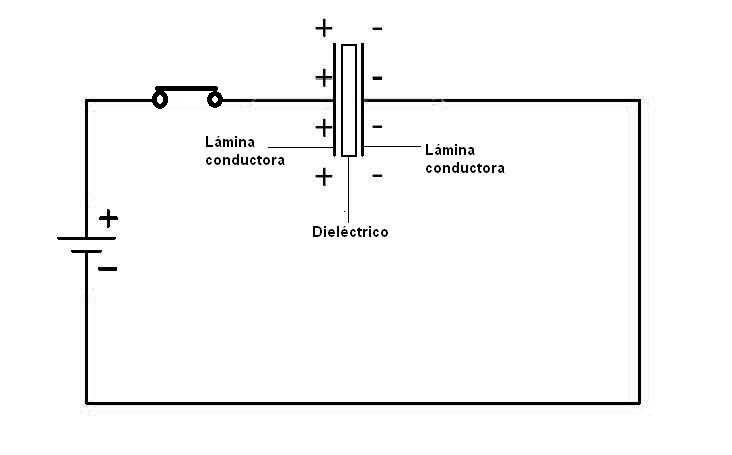 |
| Figura 1: Estructura de un condensador | Figura 2: Carga de un condensador |
La unidad de capacidad: el Faradio
La cantidad de electrones, mejor dicho culombios (nuestra unidad de cantidad de electricidad), que se pueden almacenar en un condensador es directamente proporcional a la capacidad (que se mide en Faradios) y a la tensión aplicada en voltios; es decir, es proporcional a la presión con que los apretamos, cuidando siempre que no superemos la tensión de ruptura o de perforación del dieléctrico. Así pues:
Q (culombios) = C (faradios) x V (voltios)
La capacidad C de un condensador depende de tres factores::el coeficiente dieléctrico ξ del material aislante que los separa, la superficie enfrentada S de las láminas conductoras y la distancia d que las separa.
C = ξ x S / d
En general, contra más grande es un condensador, mayor capacidad de almacenamiento tiene, pues la capacidad es directamente proporcional a la superficie enfrentada de las dos placas, Pero hay dieléctricos, como el tantalio, que aumentan mucho la capacidad, gracias a un elevadísimo coeficiente dieléctrico, por lo que con el tantalio se consiguen condensadores muy pequeños con gran capacidad.
En la práctica, esta unidad, el Faradio, es demasiado grande y las capacidades de los condensadores más usuales se miden en microfaradios (μF o millonésima de faradio o sea 10^-6 Faradios, el ,nanofaradio (nF o mil millonésima de faradio o 10^-9 Faradios y el picofaradio (pF o billonésima de faradio o 10^-12 Faradios.
Carga del condensador en corriente continua
Las tensiones y corrientes que se producen en la carga de un condensador como el de la figura 2 las podemos contemplar en la figura 3, en cuanto cerramos el interruptor, pues queda conectado el condensador a una pila o batería. La figura 3 muestra la evolución.
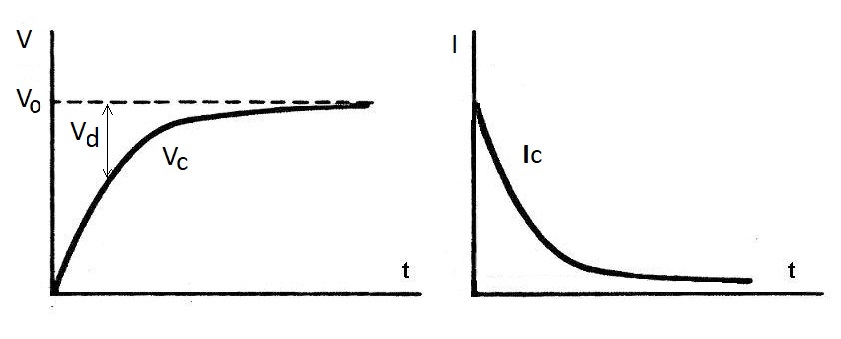 |
| Figura 3: Tensión y corriente en un condensador que se carga. |
Al cerrar el interruptor de la pila con una tensión Vo, el condensador experimente un aumento paulatino de la tensión Vc a lo largo del tiempo, hasta que alcanza con un cierto retardo prácticamente la tensión máxima Vo.
Mientras tanto, la corriente de carga Ic en el condensador ha comenzado muy fuerte, pues no encuentra apenas resistencia y está solo limitada por la resistencia interna de la pila y de los cables de conexión pero, a medida que se carga el condensador, va disminuyendo muy rápidamente la corriente Ic, porque cada vez es menor la tensión Vd diferencial que la empuja, porque hay menos diferencia de tensiones entre el voltaje de pila Vo (que presiona los electrones) y la tensión del condensador Vc, que ya se va cargando poco a poco, aumenta su tensión y se resiste a admitir más electrones (Vd = Vo –Vc) al aumentar su tensión o presión, porque ya no caben más.
El resultado es que la corriente Ic es muy grande al principio, justo cuando la tensión en el condensador es muy pequeña y disminuye poco a poco a medida que aumenta la tensión en el condensador. En resumen, en pocas palabras: la corriente es grande cuando la tensión es pequeña y es pequeña cuando la tensión es mayor. Las dos NO evolucionan al mismo tiempo.
El condensador en corriente alterna
Los condensadores dejan pasar la corriente alterna a pesar de tener una lámina aislante en su interior. ¿Cómo es eso posible? La sorprendente propiedad de los condensadores es que se comportan como si la corriente los atravesara, aunque no pase ni un electrón de una placa a otra porque lo impide el aislante, pero los electrones se mueven en el circuito igual como si pasaran; es decir, se mueven hacia delante para entrar en el condensador y hacia atrás para salir del condensador (figura 4), al ritmo que le marca la tensión alterna que cambia de signo y, por tanto, este movimiento electrónico es realmente una corriente alterna, que enciende la bombilla casi exactamente igual (figura 5) que si no estuviera el condensador.
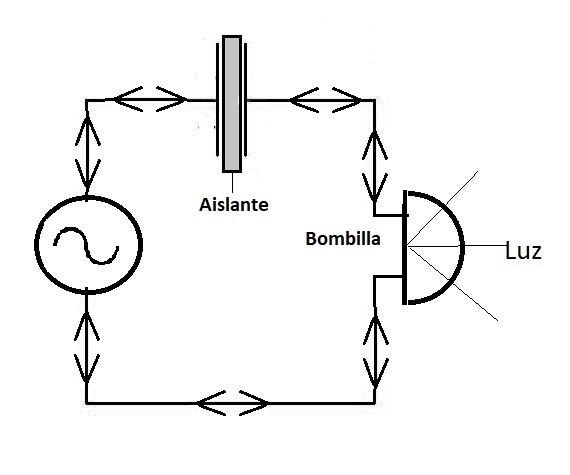 |
| Figura 4: La bombilla se enciende con el condensador |
Aunque realmente los electrones no circulan ni traspasan el dieléctrico, pero como realmente entran y salen de las armaduras del condensador, se comportan a todos los efectos como si lo atravesaran, pues hay una corriente alterna de electrones que cargan, descargan y vuelven a cargar el condensador con tensión opuesta, porque entran y salen de sus armaduras. Ese movimiento produce en la bombilla efectos casi idénticos a los de una corriente alterna que circulara por la bombilla sin condensador, como si la corriente atravesara el condensador. No hay casi diferencia.
Reactancia capacitiva
De todas maneras, hemos puntualizado siempre “casi”, porque tenemos que advertir que el paso aparente de la corriente alterna por un condensador no es un paso totalmente franco, sino que el condensador presenta una cierta oposición a su paso, porque realmente añade una dificultad al paso de la corriente que llamamos reactancia capacitiva.
La reactancia capacitiva al paso de la corriente alterna se representa por el símbolo Xc y se mide también en ohmios, pero no se transforma en pérdida de energía en forma de calor como en una resistencia, porque con la reactancia los electrones no calientan el condensador como se produce en una resistencia que calienta su entorno. Los electrones no pierden energía por causa del condensador.
La dificultad al paso de la corriente que opone el condensador se debe a que no pasan los mismos electrones que pasarían por la bombilla si no estuviera intercalado, sino que esta corriente queda limitada por la cantidad de electrones que pueden entrar y salir del condensador en cada ciclo alterno; es decir, la capacidad del condensador limita esa corriente, aunque por otra parte podemos favorecerla e incrementarla, aumentando la frecuencia de la corriente alterna. Más cambios de sentido por segundo, más electrones que se mueven por segundo. Ambos factores, capacidad y frecuencia, actúan disminuyendo esta reactancia capacitiva cuando los aumentamos y, por tanto, aparecen en el denominador del quebrado de la fórmula que nos calcula el valor de la reactancia: Xc = 1/ (2π x f x C) en ohmios.
Naturaleza de esta reactancia
Es evidente que esta oposición del condensador no es exactamente del mismo género que la que opone una resistencia, la cual simplemente frena los electrones y desprende calor, sino que aquí se produce un fenómeno completamente distinto, que consiste en que la capacidad del condensador limita la cantidad de electrones que pueden entrar y salir del condensador (su capacidad), pero también podemos incrementar la corriente aumentando la frecuencia de la corriente alterna.
Además, se produce un desfase entre la corriente alterna que circula y la tensión alterna que la fuerza a circular. No pulsan al mismo tiempo, sino que la forma de la corriente ADELANTA a la forma de la tensión como vemos en la figura 5, en donde la palabra “adelantar” significa que la forma de su onda de la corriente I está algo por delante de la forma de onda de la tensión V.
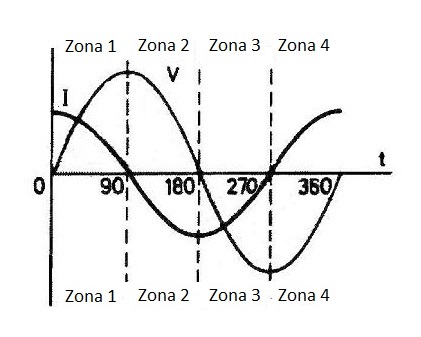 |
| Figura 5: La forma de la corriente I adelanta a la tensión V. |
En la figura 5 se observa (zona 1) que, cuando aumenta la tensión en el condensador, la corriente empieza ya a disminuir, y cuando la tensión empieza a disminuir (zona 2) la corriente cambia de signo y llega a ser opuesta, y cuando la tensión cambia de signo (zona 3) la corriente opuesta ya ha empieza a disminuir y la tensión opuesta aumenta y, finalmente, la corriente cambia de signo (zona 4) justo cuando la tensión opuesta vuelve a disminuir.
Impedancia
Se llama impedancia a la suma de la oposición producida por una resistencia y por la reactancia de un condensador, ambos conectados en serie y, puesto que ambas oposiciones no se pueden sumar directamente, porque son de naturaleza distinta, tienen que sumarse mediante una suma vectorial (Figura 6). Esta suma vectorial de la R y la Xc se indica por la letra “j” que se antepone a la reactancia (jXc) y se maneja matemáticamente con lo que se denominan “números complejos”. La reactancia Xc se considera de signo negativo.
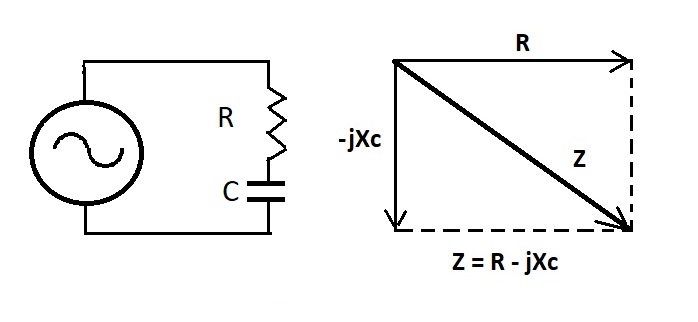 |
| Figura 6: Suma vectorial de la resistencia R y de la reactancia Xc |
El signo negativo se debe a que la reactancia capacitiva es opuesta a la reactancia inductiva que veremos a continuación y porque ésta última se considera positiva, Las dos son de signo opuesto y se pueden contrarrestar directamente entre sí, mientras que la resistencia se busca la vida por su cuenta y no hay resistencias negativas, porque la energía que se pierde en una resistencia nunca refrigera sino que siempre calienta y desprende calor.
El valor del vector reactancia Z es la hipotenusa de un triángulo rectángulo formado por R y Xc, de forma que se cumple la relación de Pitágoras en el triángulo rectángulo y Z2 = R2 + Xc2 .
La inductancia de una bobina
Una bobina es un componente pasivo que está formado por un hilo conductor enrollado en espiras devanadas en el aire o sobre un cilindro (Figura 7). El efecto de dar varias vueltas a un hilo conductor sobre un cilindro provoca que se sumen los campos magnéticos generados por cada una de las espiras, cuando por el hilo del bobinado circula una corriente y se multiplique el flujo magnético por el número de espiras del bobinado en el eje central de la bobina.
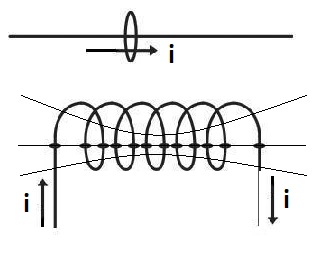 |
| Figura 7. Campo magnético en el eje central de una bobina |
La bobina almacena energía eléctrica en forma de campo magnético, de un modo análogo a la acumulación de cargas eléctricas del condensador (en forma de campo eléctrico). Ya podemos imaginar que esto tendrá consecuencias cuando le apliquemos corrientes y tensiones alternas.
La autoinducción
La autoinducción en una inductancia o bobina es el efecto que se produce en una bobina cuando el campo magnético creado por la corriente que pasa por una espira, se suma al de todas las demás espiras de la bobina, incrementando el campo magnético común, en el que se acumula energía por el paso de una corriente continua.
El campo magnético resultante de todas las espiras se comporta como un acumulador de energía similar a la acumulación de cargas en un condensador y, del mismo modo, el campo magnético devuelve esta energía cuando se retira la corriente inductora.
Al conectar la bobina a una tensión Vo continua, la corriente IL sube lentamente porque aparece una tensión inducida contraria (llamada fuerza contra-electromotriz) generada en todas las espiras y que por culpa de la autoinducción se opone al aumento de la corriente, generando una tensión opuesta a la de fuente. Esto impide el aumento rápido de la corriente que aumenta lentamente.
Esta tensión que se opone al incremento de la corriente es equivalente a la tensión con la que se va cargando el condensador y que se opone a que entren más cargas porque ya está aumentando la presión en las placas del condensador. Si os fijáis en la figura 8 veréis que esta ilustración es muy similar a la del condensador de la figura 3, pero opuesta en cuanto a corrientes y tensiones, pues donde antes había corrientes que disminuían ahora hay tensiones y viceversa.
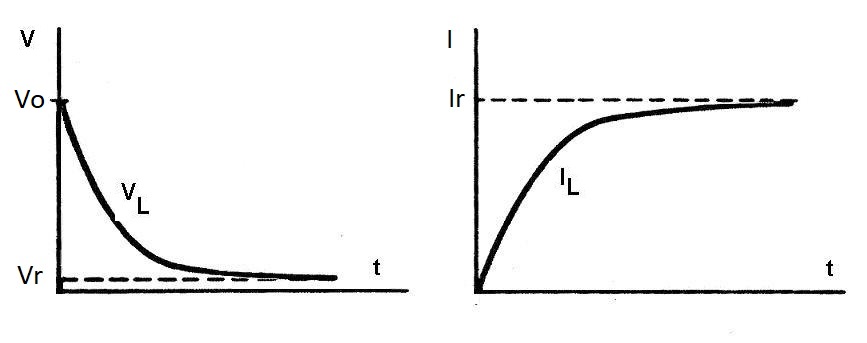 |
| Figura 8: Corriente IL en una bobina al conectarla a una pila de tensión Vo. |
El resultado es que la corriente IL es muy pequeña al principio, justo cuando la tensión Vo en la bobina es muy grande y aumenta poco a poco a medida que disminuye la tensión en bornes de la bobina y queda una tensión residual Vr debida a la resistencia del hilo de la bobina. En resumen, en pocas palabras: la corriente es pequeña cuando la tensión es grande y la corriente es grande cuando la tensión es pequeña. Las dos no evolucionan al mismo tiempo, igual que en el condensador, pero de modo opuesto.
Unidad de inductancia: el Henrio
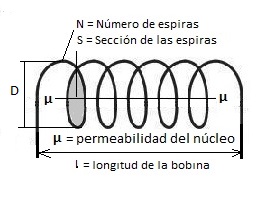
En la autoinducción o inductancia L de una bobina, en primer lugar influye favorablemente el número de espiras N, pues cuanto más espiras mayor será la autoinducción. También influye positivamente el diámetro D, pues cuanto mayor sea el diámetro de la bobina también mayor será la inductancia.
 |
| Figura 9: Cálculo de la autoinducción |
En cambio, contra mayor sea longitud del arrollamiento l y más distanciadas estén las espiras, menor será la inductancia, pues disminuye la autoinducción mutua entre espiras. Así que cuanto más pequeña sea la distancia entre espiras, mayor será la autoinducción. Por último, también afecta a la inductancia si está enrollada sobre un núcleo de aire o el núcleo es ferromagnético con una permeabilidad magnética µ superior a la del aire y que refuerce el campo magnético. La fórmula que nos proporciona la inductancia es la siguiente:
L ( µH ) = µ x 0.394 x D2 x N2 / ( 18 x D + 40 x l )
Pero lo único que nos interesa recordar aquí es la unidad de inductancia que se mide en Henrios (Hy), aunque en la práctica el Henrio es una unidad muy grande y se utiliza mucho más el milihenrio (0,001 o 10-3Hy) y el microhenrio ( 0,000.001 o 10-6 Hy) .
Reactancia inductiva e impedancia
Para una corriente continua, la bobina al cabo de poco tiempo no opone apenas más resistencia que la pequeñísima resistencia del hilo que la constituye, pues se comporta como lo que es, simplemente un trozo de hilo conductor, o sea, presenta una muy pequeña resistencia óhmica que se opone a la corriente, como todo conductor que no sea superconductor.
Pero en cuanto se intenta hacer pasar una corriente alterna por una bobina, aparece una oposición adicional a las variaciones de corriente y al paso de esta corriente alterna, y esta oposición aumenta con la inductancia y con la frecuencia de la corriente alterna y se llama reactancia inductiva.
La energía acumulada en el campo magnético se opone a las variaciones de la corriente alterna. Si intenta disminuir, pretende que no disminuya entregando energía y, si intenta aumentar, se opone a que aumente.
La fórmula que relaciona la frecuencia de la corriente alterna y la oposición que presenta una bobina de valor L a su paso y que llamamos reactancia es la siguiente:
XL = 2 x π x f x L
Si la frecuencia es igual a 0, esto significa que la corriente es continua y, como se puede apreciar en la fórmula, la reactancia será nula, pues XL = 2 x π x 0 x L = 0, tal y como habíamos comentado, cuando decíamos que para la corriente continua la oposición que presenta sólo es la resistencia del hilo. Se observa claramente que la reactancia inductiva aumentará cuando se aumente la frecuencia de un modo totalmente proporcional.
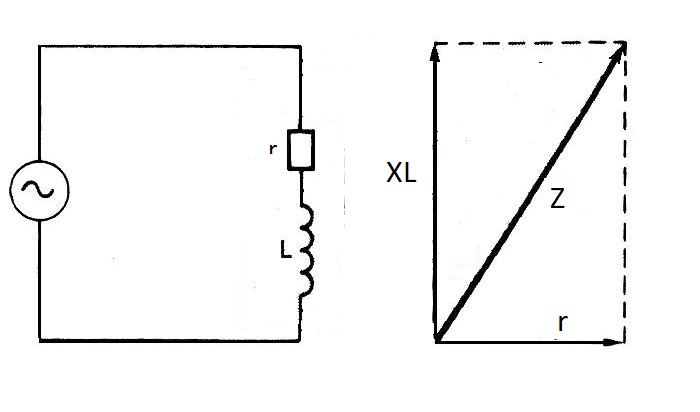
En una bobina también existe la resistencia del hilo del enrollamiento, de modo que ahora introducimos el concepto de impedancia Z de una bobina que se compone de la suma de la resistencia r del hilo y la reactancia inductiva de la bobina (figura 10).
ZL = r + jXL = r + j 2 π f L
Aquí vemos aquí también aparece una letra j que es un operador que nos indica que esta suma no es una suma normal, sino que es una suma vectorial. No se pueden sumar directamente los ohmios de la resistencia r y los ohmios de la reactancia XL, porque son de distinta naturaleza, sino que hay que sumarlos vectorialmente como los catetos de un triángulo rectángulo o matemáticamente como números complejos (Figura 10). Pero no necesitamos saber tanto para manejarla.
 |
| Figura 10: suma vectorial de reactancia inductiva y resistencia |
Retraso de la corriente respecto a la tensión
Como las variaciones del campo magnético son producidas por las variaciones de una corriente variable, estas variaciones son las que generan la tensión contraria (fuerza contra electromotriz) que se opone a los cambios de la corriente y consigue que estos cambios en la corriente se produzcan más tarde que los de la tensión o sea con retraso.
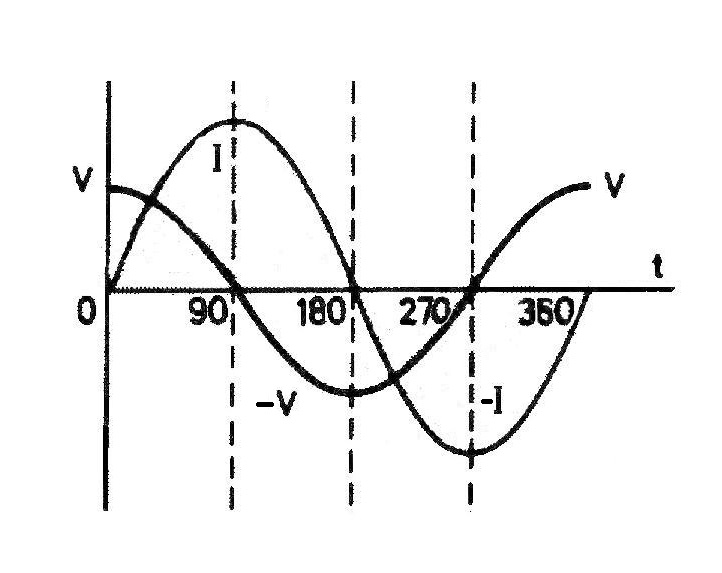
De modo que descubrimos que la pulsación o fase de la corriente que pasa por una bobina o autoinducción está retrasada en relación a la forma de variar de la tensión alterna.
 |
| Figura 11: En una inductancia, la corriente se retrasa |
Veamos con más detalle lo que ocurre en la bobina de la figura 11;
(t=0º) En cuanto aplicamos una tensión V, comienza a intentar circular una corriente y, esta corriente genera una tensión opuesta que dificulta que aumente la corriente I de tal modo que la corriente aumenta muy lentamente y alcanza su máximo cuando ya la tensión inicial llega a cero (t=90º) y empieza a invertir su signo.
(t=90º) La tensión ha cambiado de signo, pero la bobina se resiste a la disminución de la corriente alcanzada, de modo que se produce con cierto retraso de modo que solo se anula cuando ya la tensión ha llegado a su máximo negativo ((t=180º)..
(t=180º) La tensión de signo opuesto ha alcanzado al máximo y por fin la corriente empieza a cambiar de sentido y se incrementa en sentido opuesto hasta llegar a su valor máximo negativo (t=270º)
(t=270º) Mientras tanto, la tensión ha disminuido y se ha anulado totalmente y empieza a aumentar con su sentido inicial hasta volver al máximo inicial y la corriente opuesta disminuye y casi se anula (t=360º).
(t=360º) Volvemos a iniciar el ciclo (t=0º).
Antenas largas y cortas
Así que como ya sabes que estos retrasos y adelantos se deben a reactancias inductivas y a las capacitivas, no te extrañará que te contemos que, cuando una antena dipolo de media onda es demasiado larga (figura 12) , en su centro aparece, además de la resistencia de radiación Rr, una reactancia inductiva adicional. Ahora ya sabes que lo que estamos diciendo es que la corriente en el centro de la antena se ha retrasado en relación a la tensión que le suministramos por el coaxial, porque los electrones (realmente la tacada repulsiva) que rebotan en la punta de la antena porque no pueden salir, vuelven algo retrasados y llegan tarde y fuera de fase al centro de la antena y ahora la impedancia de la antena en el centro es algo mayor, porque hay que añadir la reactancia inductiva y ahora vale Z = Rr + jXL(Figura 12).
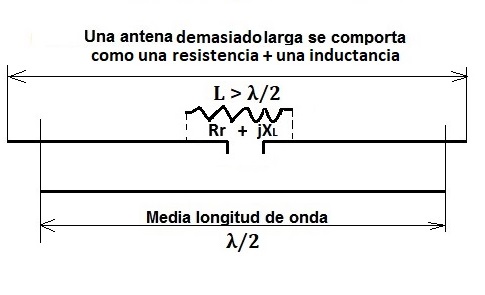 |
| Figura 12: Una antena demasiado larga presenta reactancia inductiva en su centro. |
También así entenderás mejor que, cuando una antena dipolo de media onda es demasiado corta (figura 12), entonces aparece en su centro además de la resistencia de radiación Rr, una reactancia capacitiva, y sabrás inmediatamente que lo que estamos diciendo es que la corriente en el centro de la antena se ha adelantado en relación a la tensión que le suministramos por el coaxial, porque los electrones (realmente la tacada repulsiva) que rebotan en la punta de la antena porque no pueden salir, ahora vuelven ligeramente adelantados, antes de tiempo y fuera de fase, al centro de la antena, y ahora la impedancia de la antena hay que sumarle (con signo menos) la reactancia capacitiva o sea Z = Rr –jXC (figura 13).
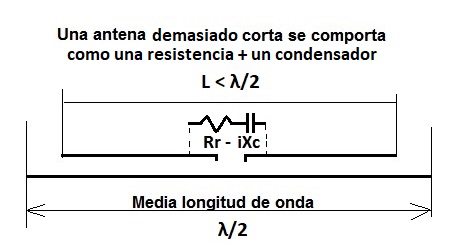 |
| Figura 13: Una antena demasiado corta presenta reactancia capacitiva en su centro. |
Espero y confío en que con estas explicaciones ahora se comprenda mejor el capítulo “La ROE en HF y VHF+”, nº 7º de EL ABC DE LAS ANTENAS, con lo que ya me quedaré más tranquilo de que habiendo leído este texto, su lectura será más fácil y relajada para todos.
73 de Luis EA3OG

